Oribital parameters explained
Name
Name given to the satellite by its creator.
Norad
The Satellite Catalog Number (also known as NORAD Catalog Number, NASA catalog number, USSPACECOM object number or simply Catalog number and similar variants) is a sequential 5-digit number assigned by USSPACECOM to all Earth orbiting satellites in order of identification. Before USSPACECOM, the catalog was maintained by NORAD. The first catalogued object, catalog number 00001, is the Sputnik 1 launch vehicle.
COSPAR designation
The International Designator, also known as COSPAR designation, and in the United States as NSSDC ID, is an international naming convention for satellites. It consists of the launch year, a 3-digit incrementing launch number of that year and up to a 3-letter code representing the sequential identifier of a piece in a launch.
Inclination
[aka “Inclination” or “I0”]
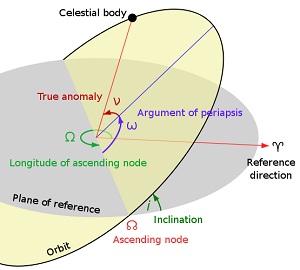The orbit ellipse lies in a plane known as the orbital plane. The orbital plane always goes through the center of the earth, but may be tilted any angle relative to the equator. Inclination is the angle between the orbital plane and the equatorial plane. By convention, inclination is a number between 0 and 180 degrees.
Some vocabulary: Orbits with inclination near 0 degrees are called equatorial orbits (because the satellite stays nearly over the equator). Orbits with inclination near 90 degrees are called polar (because the satellite crosses over the north and south poles). The intersection of the equatorial plane and the orbital plane is a line which is called the line of nodes. More about that later.
RAAN (Right Ascension of Ascending Node)
[aka “RAAN” or “RA of Node” or “O0”, and occasionally called “Longitude of Ascending Node”]
RAAN wins the prize for most horribly named orbital element. Two numbers orient the orbital plane in space. The first number was Inclination. This is the second. After we’ve specified inclination, there are still an infinite number of orbital planes possible. The line of nodes can poke out the anywhere along the equator. If we specify where along the equator the line of nodes pokes out, we will have the orbital plane fully specified. The line of nodes pokes out two places, of course. We only need to specify one of them. One is called the ascending node (where the satellite crosses the equator going from south to north). The other is called the descending node (where the satellite crosses the equator going from north to south). By convention, we specify the location of the ascending node.
Now, the earth is spinning. This means that we can’t use the common latitude/longitude coordinate system to specify where the line of nodes points. Instead, we use an astronomical coordinate system, known as the right ascension / declination coordinate system, which does not spin with the earth. Right ascension is another fancy word for an angle, in this case, an angle measured in the equatorial plane from a reference point in the sky where right ascension is defined to be zero. Astronomers call this point the vernal equinox.
Finally, “right ascension of ascending node” is an angle, measured at the center of the earth, from the vernal equinox to the ascending node.
I know this is getting complicated. Here’s an example. Draw a line from the center of the earth to the point where our satellite crosses the equator (going from south to north). If this line points directly at the vernal equinox, then RAAN = 0 degrees.
By convention, RAAN is a number in the range 0 to 360 degrees.
I used the term “vernal equinox” above without really defining it. If you can tolerate a minor digression, I’ll do that now. Teachers have told children for years that the vernal equinox is “the place in the sky where the sun rises on the first day of Spring”. This is a horrible definition. Most teachers, and students, have no idea what the first day of spring is (except a date on a calendar), and no idea why the sun should be in the same place in the sky on that date every year.
You now have enough astronomy vocabulary to get a better definition. Consider the orbit of the sun around the earth. I know in school they told you the earth orbits around the sun, but the math is equally valid either way, and it suits our needs at this instant to think of the sun orbiting the earth. The orbit of the sun has an inclination of about 23.5 degrees. (Astronomers don’t usually call this 23.5 degree angle an ‘inclination’, by the way. They use an infinitely more obscure name: The Obliquity of The Ecliptic.) The orbit of the sun is divided (by humans) into four equally sized portions called seasons. The one called Spring begins when the sun pops up past the equator. In other words, the first day of Spring is the day that the sun crosses through the equatorial plane going from South to North. We have a name for that! It’s the ascending node of the Sun’s orbit. So finally, the vernal equinox is nothing more than the ascending node of the Sun’s orbit. The Sun’s orbit has RAAN = 0 simply because we’ve defined the Sun’s ascending node as the place from which all ascending nodes are measured. The RAAN of your satellite’s orbit is just the angle (measured at the center of the earth) between the place the Sun’s orbit pops up past the equator, and the place your satellite’s orbit pops up past the equator.
Eccentricity
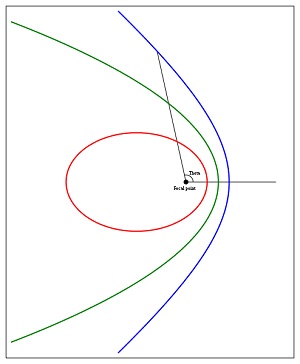[aka “ecce” or “E0” or “e”]
This one is simple. In the Keplerian orbit model, the satellite orbit is an ellipse. Eccentricity tells us the “shape” of the ellipse. When e=0, the ellipse is a circle. When e is very near 1, the ellipse is very long and skinny.
(To be precise, the Keplerian orbit is a conic section, which can be either an ellipse, which includes circles, a parabola, a hyperbola, or a straight line! But here, we are only interested in elliptical orbits. The other kinds of orbits are not used for satellites, at least not on purpose, and tracking programs typically aren’t programmed to handle them.) For our purposes, eccentricity must be in the range 0 <= e < 1.
ARGP
[aka “ARGP” or “W0”]
Argument is yet another fancy word for angle. Now that we’ve oriented the orbital plane in space, we need to orient the orbit ellipse in the orbital plane. We do this by specifying a single angle known as argument of perigee.
A few words about elliptical orbits… The point where the satellite is closest to the earth is called perigee, although it’s sometimes called periapsis or perifocus. We’ll call it perigee. The point where the satellite is farthest from earth is called apogee (aka apoapsis, or apifocus). If we draw a line from perigee to apogee, this line is called the line-of-apsides. (Apsides is, of course, the plural of apsis.) I know, this is getting complicated again. Sometimes the line-of-apsides is called the major-axis of the ellipse. It’s just a line drawn through the ellipse the “long way”.
The line-of-apsides passes through the center of the earth. We’ve already identified another line passing through the center of the earth: the line of nodes. The angle between these two lines is called the argument of perigee. Where any two lines intersect, they form two supplementary angles, so to be specific, we say that argument of perigee is the angle (measured at the center of the earth) from the ascending node to perigee.
Example: When ARGP = 0, the perigee occurs at the same place as the ascending node. That means that the satellite would be closest to earth just as it rises up over the equator. When ARGP = 180 degrees, apogee would occur at the same place as the ascending node. That means that the satellite would be farthest from earth just as it rises up over the equator.
By convention, ARGP is an angle between 0 and 360 degrees
Orbit per day
Number of times a satellite orbits the earth.
Period
The time it takes to orbit the earth one time.
Semi-major axis
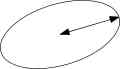The major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape. The semi-major axis is one half of the major axis, and thus runs from the centre, through a focus, and to the edge of the ellipse; essentially, it is the measure of the radius of an orbit taken at the orbit’s two most distant points. For the special case of a circle, the semi-major axis is the radius. One can think of the semi-major axis as an ellipse’s long radius.
Perigee x apogee
Apogee and perigee refer to the distance from the Earth to the object. Apogee is the furthest point from the earth. Perigee is the closest point to the earth.
Mean anomaly
[aka “M0” or “MA” or “Phase”]
Now that we have the size, shape, and orientation of the orbit firmly established, the only thing left to do is specify where exactly the satellite is on this orbit ellipse at some particular time. Our very first orbital element (Epoch) specified a particular time, so all we need to do now is specify where, on the ellipse, our satellite was exactly at the Epoch time.
Anomaly is yet another astronomer-word for angle. Mean anomaly is simply an angle that marches uniformly in time from 0 to 360 degrees during one revolution. It is defined to be 0 degrees at perigee, and therefore is 180 degrees at apogee.
If you had a satellite in a circular orbit (therefore moving at constant speed) and you stood in the center of the earth and measured this angle from perigee, you would point directly at the satellite. Satellites in non-circular orbits move at a non-constant speed, so this simple relation doesn’t hold. This relation does hold for two important points on the orbit, however, no matter what the eccentricity. Perigee always occurs at MA = 0, and apogee always occurs at MA = 180 degrees.
It has become common practice with radio amateur satellites to use Mean Anomaly to schedule satellite operations. Satellites commonly change modes or turn on or off at specific places in their orbits, specified by Mean Anomaly. Unfortunately, when used this way, it is common to specify MA in units of 256ths of a circle instead of degrees! Some tracking programs use the term “phase” when they display MA in these units. It is still specified in degrees, between 0 and 360, when entered as an orbital element.
Example: Suppose Oscar-99 has a period of 12 hours, and is turned off from Phase 240 to 16. That means it’s off for 32 ticks of phase. There are 256 of these ticks in the entire 12 hour orbit, so it’s off for (32/256)x12hrs = 1.5 hours. Note that the off time is centered on perigee. Satellites in highly eccentric orbits are often turned off near perigee when they’re moving the fastest, and therefore difficult to use.